[Paper Review] Denoising Diffusion Probabilistic Models (NeurIPS 2020)
Denoising Diffusion Probabilistic Models (NeurIPS 2020)
Denoising Diffusion Probabilistic Models. [Paper] [Github]
Jonathan Ho, Ajay Jain, Pieter Abbeel
Jun 19th 2020
Diffusion Model의 (거의) 시작점을 알린 논문이다. 이 논문을 처음 보았을 때 굉장히 어려웠었고, 그래서 이 논문을 가장 먼저 포스팅해보려고 한다. 혹시 관련 개념을 잘 모른다면, [Intro to Diffusion Models] (1) What is Diffusion?를 보고 오시는 것을 추천한다.
또한, Diffusion Model의 수학을 굉장히 잘 설명해둔 Understanding Diffusion Models: A Unified Perspective 역시 큰 도움이 될 것이다. 이 포스팅의 전개 부분은 위 논문을 많이 참고하였다. 이 포스팅에서 Understanding Diffusion Models: A Unified Perspective에 대해 다루지 않은 내용은 추후에 리뷰할 예정이다.
Background
Diffusion Model은 다음과 같은 형태를 띈다.
\[x_0:=x(0)\sim p_{data}(x)\underset{p_\theta(x_0 \vert x_1)}{\overset{q(x_1 \vert x_0)}{\rightleftarrows}} x_1 \rightleftarrows \cdots \rightarrow x_{T-1} \underset{p_\theta(x_{T-1} \vert x_{T})}{\overset{q(x_{T} \vert x_{T-1})}{\rightleftarrows}} x_T:=x(1),\ x(1)\approx z\sim \mathcal N(0,I)\]이를 모델 $p_\theta$의 관점에서 표현하면, Reverse Diffusion Process를 묘사하는 다음의 latent variable model로 표현된다.
\[p_\theta(x_{0:T}):=p(x_T)\prod^T_{t=1}p_\theta(x_{t-1}\vert x_t),\quad p_\theta(x_{t-1}\vert x_t)=\mathcal N(x_{t-1}; \mu_\theta(x_t,t),\Sigma_\theta(x_t,t))\]이때, $p_\theta(x_{0:T})$는 posterior이자, Forward Diffusion Process인
\[q(x_{1:T}\vert x_0):=\prod^T_{t=1}q(x_t\vert x_{t-1}),\quad q(x_t\vert x_{t-1}):=\mathcal N(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_t I)\]를 근사하도록 학습한다.
Reverse Diffusion Process로 왜 Forward Diffusion Process를 근사하는가?
이때, $q(x_T\vert x_0)\approx \mathcal N(x_T;0,I)$여야 하기 때문에, $q(x_t\vert x_{0})$은 $t\rightarrow T$로 진행될 수록 $x_{t-1}$의 영향력을 줄여나가면서, variance를 $I$에 가깝게 만들어야 한다. 따라서 variance schedule, $\beta_1,\dots,\beta_T$는 $0<\beta_1,<\beta_2<\cdots<\beta_{T-1}<\beta_T<1$ 로 정의된다. 따라서, 이 과정을 거치면, $x_{t-1}$을 scaling down 하고 gaussian noise를 더하는 형태로 Diffusion Process를 진행하게 된다. 이때, variance scheduling ($\beta_t$)의 설정은 논문마다 다르며, 이후 논문들에서는 효과적인 variacne scheduling을 찾기 위한 노력을 하기도 한다.
학습은 variational bound on negative log-likelihood를 최적화하여 $p_\theta$를 학습한다.
\[\begin{align} \mathbb E\left[{-\log p_\theta(x_{0})}\right] &\leq \mathbb E_{q}\left[{ - \log \frac{p_\theta(x_{0:T})}{q(x_{1:T} | x_0)}}\right] \\ & = \mathbb{E}_q\left[ -\log p(x_T) - \sum_{t \geq 1} \log \frac{p_\theta(x_{t-1} | x_t)}{q(x_t|x_{t-1})} \right] := L \end{align}\]이때, $\leq$는 Jensen’s inequality에 의해 성립된다. $L$을 최적화하는 것은 $\log p_\theta(x_{0})$을 최대화하는 것과 같으므로, data $x_0$을 sampling할 확률을 높이는 방향으로 $p_\theta$를 학습한다는 뜻이다.
Reparameterization trick
왜 gaussian noise를 더한다는 것인가? 이는 gaussian distribution에서의 sampling 과정을 살펴보면 명확해진다. (statistical machine learning에서 주로 쓰이며) 딥러닝에서는 VAE 논문에서 사용하여 유명해진 Reparameterization trick을 사용하여 gaussian distribution에서의 sampling을 진행한다. Back-propagation을 통해 gaussian distribution을 묘사하는 $\mu,\sigma^2$을 학습하기 위해서는, $\mu,\sigma$에 gradient가 흐르도록 $z\sim\mathcal N(\mu,\sigma^2)$을 sampling 해야한다. Reparameterization trick은 $z$를 다음과 같은 형태로 샘플링한다.
\[z=\mu+\sigma\epsilon,\quad \epsilon\sim \mathcal N(0,I)\]이 형태를 고려하여 $q(x_t\vert x_{t-1}):=\mathcal N(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_t I)$를 살펴보면
\[x_t=\sqrt{1-\beta_t}x_{t-1}+\beta_t I\epsilon_t,\quad \epsilon_t\sim \mathcal N(0,I)\]형태를 띈다. $0<\beta_t<1$ 이기 때문에, $x_t$에서 $x_{t-1}$은 scaling down되고, $\beta_t$만큼 scaling된 gaussian noise $\epsilon_t$가 $\sqrt{1-\beta_t}x_{t-1}$에 더해진 형태로 $x_t$가 sampling 되는 것이다.
Toward Efficients Experssions for Diffusion Model Training
만약 $x_t$에 대해서 학습하기 위해서 모든 $x_0,x_1,\dots,x_{t-1}$의 diffusion step을 거쳐야한다면 굉장히 오랜 시간이 걸릴 것이다. DDPM에서는 임의의 time step $t$에 대해 $x_t$를 샘플링할 수 있는 closed form을 보였다.
\[q(x_t\vert x_0)=\mathcal N(x_t;\sqrt{\bar \alpha_t}x_0,(1-\bar\alpha_t)I)\]이때, $\alpha_t:=1-\beta_t$, $\bar\alpha_t:=\prod^t_{s=1}\alpha_s$ 이다.
Derivation for $q(x_t \vert x_0)$
위 식을 이용하여, data $x_0$에서 임의의 time step $t$의 $x_t$를 직접적으로 샘플링이 가능하기 때문에 효율적으로 학습이 가능하다.
한가지 기억할 점은, 우리의 모델 $p_\theta(x_{t-1}\vert x_t)$는 $x_t$를 input으로 받아 $x_{t-1}$을 예측하는 모델이기 때문에, 이를 학습시키기 위한 target $x_{t-1}$을 forward diffusion distribution $q(\cdot)$에서 샘플링할 수 있어야 한다. 위 식을 더욱 전개하여 posteior distribution $q(x_{t-1}\vert x_t,x_0)$을 얻을 수 있다.
Bayes’ rule에 따라,
\[\underbrace{q(x_{t-1}\vert x_{t},x_0)}_{posterior}=\frac{\overbrace{q(x_t\vert x_{t-1},x_0)}^{likelihood}\overbrace{q(x_{t-1}\vert x_0)}^{prior}}{\underbrace{q(x_t\vert x_0)}_{evidence}}=\frac{q(x_t\vert x_{t-1})q(x_{t-1}\vert x_0)}{q(x_t\vert x_0)}\]$q(x_t\vert x_{t-1}, x_0)$은 Markov Process를 가정하였기 때문에 $q(x_t\vert x_{t-1},x_0)=q(x_t\vert x_{t-1})$와 동일하다.
normalization term을 배제하면 위 식은 다음 관계를 가지게 된다.
\(\begin{align} & \frac{q(x_t\vert x_{t-1},x_0)q(x_{t-1}\vert x_0)}{q(x_t\vert x_0)} \\ & \propto \exp\bigg(-\frac{1}{2}\bigg( \frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{\beta_t} + \frac{(x_{t-1}-\sqrt{\bar\alpha_{t-1}}x_0)^2}{1-\bar\alpha_{t-1}}-\frac{(x_t-\sqrt{\bar\alpha_t}x_0)^2}{1-\bar\alpha_t}\bigg)\bigg) \\ &=\exp\bigg(-\frac{1}{2}\bigg( \frac{x_{t}^2-2\sqrt{\alpha_{t}}x_tx_{t-1}+\alpha_tx_{t-1}^2}{\beta_t}+\frac{x_{t-1}^2-2\sqrt{\bar\alpha_{t-1}}x_{t-1}x_0+\bar\alpha_{t-1}x_0^2}{1-\bar\alpha_{t-1}}-\frac{x_t^2-2\sqrt{\bar\alpha_t}x_tx_0+\bar\alpha_tx_0^2}{1-\bar\alpha_t}\bigg)\bigg) \\ &= \exp\left( -\frac{1}{2}\left(\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_t}\right)x_{t-1}^2 - \left( \frac{2\sqrt{\alpha_t}}{\beta_t}x_t+\frac{2\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}x_0 \right)x_{t-1}+C(x_t,x_0) \right)\right) \\ &= \exp\left( -\frac{1}{2}\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}} \right)\left( x_{t-1}^2-2\frac{\left( \frac{\sqrt{\alpha_t}}{\beta_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}x_0 \right)}{\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}} \right)}x_{t-1}+C(x_t,x_0) \right) \right) \\ \end{align}\) 이때, $C(x_t,x_0)$은 $x_t,x_0$으로 이루어져 있는 constant term이다. 위 식으로부터 우리는 다음 식을 얻을 수 있다.
\[q(x_{t-1}\vert x_t,x_0)=\mathcal N(x_{t-1};\tilde\mu_t(x_t,x_0),\tilde\beta_tI)\] \[\begin{align*} \tilde\beta_t&=\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}} \right)^{-1}=\left( \frac{\alpha_t\left( 1-\bar\alpha_{t-1}+\beta_t \right)}{ \beta_t\left( 1-\bar\alpha_{t-1} \right)} \right)^{-1}=\left( \frac{\alpha_t-\alpha_t\bar\alpha_{t-1}+\beta_t}{ \beta_t\left( 1-\bar\alpha_{t-1} \right)} \right)^{-1}\\ &=\left( \frac{\alpha_t-\bar\alpha_t+1-\alpha_t}{ \beta_t\left( 1-\bar\alpha_{t-1} \right)} \right)^{-1}=\left( \frac{1-\bar\alpha_t}{\beta_t\left(1-\bar\alpha_{t-1}\right)} \right)^{-1}=\left(\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\right)\beta_t \\ \tilde\mu_t(x_t,x_0)&=\frac{\frac{\sqrt{\bar\alpha_t}}{\beta_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}x_0}{\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}}=\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}} \right)^{-1}\left( \frac{\sqrt{\bar\alpha_t}}{\beta_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}x_0 \right)\\&=\left( \frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \right)\left( \frac{\sqrt{\bar\alpha_{t}}}{\beta_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}x_0 \right) \\ &=\left( \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_{t}} \right)x_0+\left( \frac{\sqrt{\bar\alpha_t}\left( 1-\bar\alpha_{t-1} \right)}{1-\bar\alpha_t} \right)x_t \end{align*}\]이 식을 사용하여, 위의 최적화 식을 다음과 같이 수정이 가능하다.
\[\require{cancel} \begin{align} & \mathbb E_{q}\left[{ - \log \frac{p_\theta(x_{0:T})}{q(x_{1:T} | x_0)}}\right]\\ &=\mathbb{E}_q\left[ -\log \frac{p(x_T)\prod^T_{t=1}p_\theta(x_{t-1}\vert x_t)}{\prod^T_{t=1}q(x_t\vert x_{t-1})} \right] \\ & =\mathbb{E}_q\left[-\log \frac{p(x_T)p_\theta(x_0\vert x_1)}{q(x_1\vert x_0)}-\log \prod^T_{t=2}\frac{p_\theta(x_{t-1}\vert x_t)}{q(x_t\vert x_{t-1})} \right] \\ & =\mathbb{E}_q\left[-\log \frac{p(x_T)p_\theta(x_0\vert x_1)}{q(x_1\vert x_0)}-\log \prod^T_{t=2}\frac{p_\theta(x_{t-1}\vert x_t)}{q(x_t\vert x_{t-1},x_0)} \right] \\ & =\mathbb{E}_q\left[-\log \frac{p(x_T)p_\theta(x_0\vert x_1)}{q(x_1\vert x_0)}-\log \prod^T_{t=2}\frac{p_\theta(x_{t-1}\vert x_t)}{\frac{q(x_{t-1}\vert x_t,x_0)q(x_t\vert x_0)}{q(x_{t-1}\vert x_0)}} \right] \\ &=\mathbb{E}_q\left[ -\log \frac{p(x_T)p_\theta(x_0\vert x_1)}{\cancel{q(x_1\vert x_0)}} -\sum^T_{t=2} \log \frac{\cancel{q(x_{t-1}\vert x_0)}}{\cancel{q(x_t\vert x_{0})}} -\sum^T_{t=2}\log \frac{p_\theta(x_{t-1}\vert x_t)}{q(x_{t-1}\vert x_t,x_0)}\right] \\ &=\mathbb{E}_q\left[ -\log p_\theta(x_0\vert x_1) -\log \frac{p(x_T)}{q(x_T\vert x_0)} -\sum^T_{t=2}\log \frac{p_\theta(x_{t-1}\vert x_t)}{q(x_{t-1}\vert x_t,x_0)} \right] \\ &= \mathbb{E}_{q(x_1\vert x_0)}\left[ -p_\theta(x_0\vert x_1)\right] -\mathbb{E}_{q(x_T\vert x_0)}\left[ \log \frac{p(x_T)}{q(x_T\vert x_0)} \right ] - \sum^T_{t=2}\mathbb{E}_{q(x_t,x_{t-1}\vert x_0)}\left[ \log \frac{p_\theta(x_{t-1}\vert x_t)}{q(x_{t-1}\vert x_t,x_0)} \right] \\ &= -\underbrace{\mathbb{E}_{q(x_1\vert x_0)}\left[\log p_\theta(x_0\vert x_1)\right]}_{reconstruction\ term,L_0}+\underbrace{D_{KL}\left( q(x_T\vert x_0)\Vert p(x_T) \right)}_{prior\ matching\ term,L_T}+\sum^T_{t=2}\underbrace{\mathbb{E}_{q(x_t\vert x_0)}\left[ D_{KL}\left( q(x_{t-1}\vert x_t,x_0)\vert )\Vert p_\theta(x_{t-1}\vert x_t) \right) \right]}_{denoising\ matching\ term,L_t} \end{align}\]How to train?
$L_t$
두 gaussian distribution의 KL Divergence는 closed form이 존재한다:
\[D_{KL}\left( \mathcal N(x;\mu_x,\Sigma_x)\Vert \mathcal N(y;\mu_y,\Sigma_y) \right) =\frac{1}{2}\left[ \log\frac{\vert\Sigma_y\vert}{\vert \Sigma_x\vert}-d+tr\left( (\Sigma^{-1}_y\Sigma_x)+\left( \mu_y-\mu_x \right)^T\Sigma_y^{-1}\left( \mu_y-\mu_x \right) \right) \right]\]모델을 학습하면서 $p_\theta(x_{t-1}\vert x_t)=\mathcal N(x_{t-1}; \mu_\theta(x_t,t),\Sigma_\theta(x_t,t))$의 $\Sigma_\theta(x_t,t)$을 학습할 수도 있지만, DDPM의 저자는 이를 pre-define된 constant term으로 사용한다. 따라서, $p_\theta(x_{t-1}\vert x_t)=\mathcal N(x_{t-1}; \mu_\theta(x_t,t),\sigma_t^2I)$를 사용한다. 이로부터 아래의 loss 식을 전개할 수 있다. (Understanding Diffusion Models: A Unified Perspective eq (87~92))
\[\begin{align} & D_{KL}\left( q(x_{t-1}\vert x_t,x_0)\vert )\Vert p_\theta(x_{t-1}\vert x_t) \right) \\ =& \mathbb{E}_q\left[\frac{1}{2\sigma^2_t}\Vert \tilde\mu_t(x_t,x_0)-\mu_\theta(x_t,t) \Vert^2\right] \end{align}\]$\mu_\theta(x_t,t)$를 통해 $\tilde\mu(x_t,x_0)=\left( \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_{t}} \right)x_0+\left( \frac{\sqrt{\bar\alpha_t}\left( 1-\bar\alpha_{t-1} \right)}{1-\bar\alpha_t} \right)x_t$를 바로 예측할 수도 있지만, 동일하게 다음의 형태를 예측할 수도 있다.
\[\mu_\theta(x_t,t)=\left( \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_{t}} \right)\hat x_\theta(x_t,t)+\left( \frac{\sqrt{\bar\alpha_t}\left( 1-\bar\alpha_{t-1} \right)}{1-\bar\alpha_t} \right)x_t\]이는 $p_\theta(x_t,t)$가 $\tilde\mu(x_t,x_0)$을 바로 예측하는 것이 아닌 ground truth $x_0$을 예측하도록 하는 것과 동일하다. 이 식을 적용하면, 위 최적화 식은 다음으로 전개된다. (Understanding Diffusion Models: A Unified Perspective eq (95~99))
\[\mathbb{E}_q\left[ \frac{1}{2\sigma_t^2}\frac{\bar\alpha_{t-1}(1-\alpha_t)^2}{(1-\bar\alpha_t)^2}\left\Vert \hat x_\theta(x_t,t)-x_0 \right\Vert^2 \right]\]또한, $x_t\sim q(x_t\vert x_0)$으로부터 $x_t(x_0,\epsilon)=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon, \epsilon\sim\mathcal N(0,I)$의 식을 얻을 수 있고, 이로부터 $x_0=\frac{x_t(x_0,\epsilon)-\sqrt{1-\bar\alpha_t\epsilon}}{\sqrt{\bar\alpha_t}}$이고, 이를 $\tilde\mu(x_t,x_0)$에 대입하면,
\[\tilde\mu(x_t,x_0)=\frac{1}{\sqrt{\alpha_t}}x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}\sqrt{\alpha_t}}\epsilon_0,\quad \epsilon_0\sim\mathcal N(0,I)\]이때, $\epsilon_0$은 $x_t\sim q(x_t\vert x_0)$를 샘플링할 때, $x_0$에 더해진 noise이다. (Understanding Diffusion Models: A Unified Perspective eq (116~124))
이로부터 $\mu_\theta(x_t,t)$를 다음과 같이 표현할 수 있다.
\[\underbrace{\mu_\theta(x_t,t)=\frac{1}{\sqrt{\alpha_t}}x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}\sqrt{\alpha_t}}\hat\epsilon_\theta(x_t,t)}_{used\ for\ sampling!}\]이를 반영하면 최적화 식은 다음과 같다.
\[\mathbb{E}_q\left[ \frac{1}{2\sigma_t^2}\frac{(1-\alpha_t)^2}{(1-\bar\alpha_t)\alpha_t}\Vert \epsilon_0-\hat\epsilon_\theta(x_t,t) \Vert^2 \right]\]이는 $x_t\sim q(x_t\vert x_0)$을 샘플링할 때 $x_0$에 더해진 노이즈 $\epsilon_0$을 예측하는 것과 같다. (Understanding Diffusion Models: A Unified Perspective eq (126~130))
최종적으로 DDPM의 저자는 noise를 예측하는 형태의 마지막 최적화 식을 기용하였고, 이 식을 이용하여 $x_0$에 더해진 noise를 제거하는 denoising 형태로 샘플링을 진행한다. 저자들은 해당 loss의 simplified 버전인
\[\mathbb{E}_q\left[ \Vert \epsilon_0-\hat\epsilon_\theta(x_t,t) \Vert^2 \right]\]을 최적화하는 것이 샘플 퀄리티에 더 도움이 된다는 것을 발견하였고, 이를 loss로 기용하였다. $\sigma_t^2$의 경우, $\sigma_t^2=\beta_t$와 $\sigma_t^2=\tilde\beta_t$ 모두 실험해보았을 때, 비슷한 효과를 얻었다고 한다.
$L_T$
$\beta_t$를 DDPM 저자들은 constant로 두었기 때문에 prior matching term은 constant이고, 학습에서 배제된다.
$L_0$
마지막 reconstruction term은 실제 이미지를 복원하는 것을 목표로한다. noise가 존재하지 않는 data인 $x_0$을 만드는 것이 목표기 때문에 $x_0$가 {0,…,255}의 픽셀 값이 [-1,1]로 linear scaling 되어있다고 가정하고, 다음 식을 최적화한다.
\[p_\theta(x_0\vert x_1)=\prod^D_{i=1}\int^{\delta_+(x^i_0)}_{\delta_-(x_0^i)}\mathcal N(x;\mu^i_\theta(x_1,1),\sigma_1^2)dx\\ \delta_+(x)=\begin{cases}\infty & \text{if } x=1 \\ x+\frac{1}{255} & \text{if } x<1 \\ \end{cases} \quad \delta_-(x)=\begin{cases} -\infty & \text{if } x=-1 \\ x-\frac{1}{255} & \text{if } x>-1 \\ \end{cases}\]이때 D는 예측하는 data $x_0$의 dimensionalty, 즉 차원이며, 픽셀 하나하나의 값을 최적화하는 것과 같다. 무슨 뜻일까? 0~255가 -1~1로 scaling되었기 때문에 $[-1, -\frac{253}{255},-\frac{251}{255},\cdots,\frac{251}{255},\frac{253}{255},1]$의 값을 가지고, 한 integer 값이 -1~1에서 차지하는 범위는 $\frac{2}{255}$이다. 해당 범위 안에 $\mu_\theta$값이 예측되면, 그 값으로 반올림될 것이다. 따라서 target $x_0^i$에 따라 해당하는 범위 안을 $\mu_\theta$가 예측될 수 있도록 해당 범위의 확률을 maximize하도는 식으로 볼 수 있다. gaussian distribution의 확률 적분값은 closed form으로 예측할 수 있으니 최적화 식은 충분히 효율적이다.
Settings & Sampling & Experiments
DDPM의 학습 세팅은 다음과 같다.
- T=1000
- $\beta_1=10^{-4},\beta_T=10^{-2}$
Training & Sampling algorithm은 다음과 같다.

Source: DDPM Project page.
이때 $x_{t-1}$은 $p_{\theta}(x_{t-1}\vert x_t)=\mathcal N(x_{t-1};\mu_\theta(x_t,t),\sigma_t^2I)$을 따라 샘플링된다. $\mu_\theta(x_{t-1}\vert x_t)$?
Negative Log-Likelihood (NLL)
NLL은 모델이 얼마나 data distribution을 잘 표현하는지 측정하는데 주로 사용한다. real data에 대한 model의 확률이기 때문에 $\log p_\theta(x)$가 높을수록 좋은 것이다. 그렇기에 NLL=$-\log p_\theta(x)$는 낮을 수록 좋다. 다른 종류의 generative model은 diffusion model처럼 progressive하게 샘플링하지 않기 때문에 NLL을 output 하나에 대해서 측정한다. 또한, NLL을 측정하는 방식은 확률 분포의 가정에 따라 다양한데, 다음 포스팅을 참고하면 좋을 것이다.
DDPM의 NLL 계산식은 $L_0$을 distortion, $L_{t\geq 1}$을 rate로 취급하여 $NLL=L_0+L_1+\cdots + L_T$로 계산하였다.
Rate & Distortion?
ChatGPT에게 물어보니 다음과 같이 rate와 distortion을 설명해주었다.
PixelCNN: Rate와 Distortion
PixelCNN에서 Rate와 Distortion은 데이터 압축 효율성과 데이터 품질 간의 트레이드오프를 설명합니다. 이 두 개념은 Negative Log-Likelihood (NLL)와 밀접한 관련이 있습니다.
1. Rate (R): 표현 비용
정의: 데이터를 표현하는 데 필요한 정보량(비트 수)을 나타냅니다.
NLL과의 관계: Rate는 데이터의 평균 NLL과 직접적으로 연관되며, 다음과 같이 계산됩니다:
R = - (1/n) ∑ log P(xᵢ | x₍<ᵢ₎)
특징:
- Rate가 낮을수록 데이터 표현이 효율적입니다.
- Rate가 높을수록 데이터를 표현하는 데 더 많은 정보량이 필요합니다.
2. Distortion (D): 데이터 손실
정의: 원본 데이터와 모델이 생성한 데이터 간의 차이를 나타냅니다.
NLL과의 관계: Distortion은 모델의 재구성 품질을 나타내며, 일반적으로 다음과 같은 방식으로 측정됩니다:
D(x, ẋ) = (1/n) ∑ (xᵢ - ẋᵢ)²
특징:
- Distortion이 낮을수록 모델이 생성한 데이터가 원본 데이터에 가깝습니다.
- Distortion이 높을수록 생성된 데이터 품질이 떨어집니다.
3. Rate-Distortion 트레이드오프
정의: Rate와 Distortion은 서로 반비례 관계에 있습니다:
- Rate가 높아지면 Distortion이 낮아지고(더 높은 품질),
- Rate가 낮아지면 Distortion이 높아집니다(더 낮은 품질).
이 관계는 다음과 같이 표현됩니다:
minimize E[D(x, ẋ)] subject to R ≤ R_max
4. PixelCNN에서의 Rate와 Distortion
PixelCNN에서는 다음과 같이 Rate와 Distortion을 해석할 수 있습니다:
- Rate: 데이터셋에 대한 평균 NLL로 계산되며, 모델이 학습한 조건부 확률로부터 결정됩니다.
- Distortion: 원본 이미지와 모델이 생성한 이미지 간의 차이를 나타내며, 품질 지표(MSE, SSIM 등)로 평가됩니다.
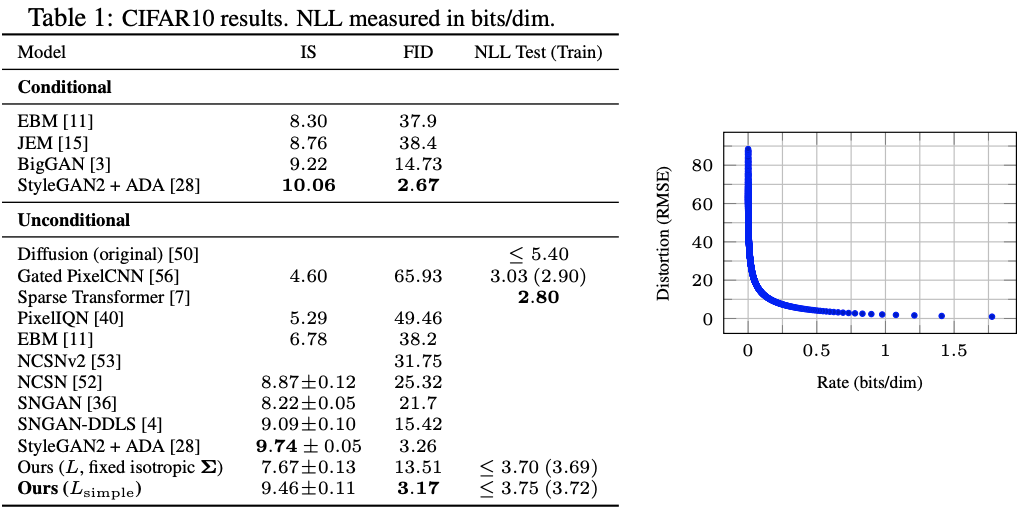
Source: DDPM Project page.
CIFAR10에서 rate: 1.78 bits/dim, distortion 1.97 bits/dim을 달성하였다.
Rate-Distortion Behavior
저자들은 Rate-Distorion Behavior를 조사하였다. (방식은 논문 내 algorithm 3&4를 참고) time step을 $t: T\rightarrow 0$으로 진행하면서 각 time step까지의 rate를 측정하였다. $(L_T\sim L_t)$ 또한, 예측된 $x_t$로부터 $x_0\approx \hat x_0=(x_t-\sqrt{1-\bar\alpha_t}0\epsilon_\theta(x_t))$를 이용하여 RMSE를 측정하였다. $(\sqrt{\Vert x_0-\hat x_0 \Vert^2/D})$.
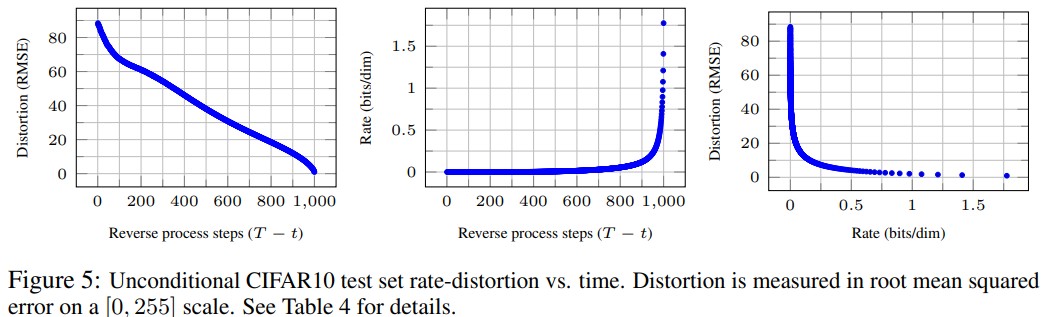
세 번째 rate vs. distortion 그래프에서 볼 수 있듯이, low-rate 영역에서 distortion이 대부분 감소한다. 반면에 high-rate region에서는 distortion이 작은 것을 알 수 있는데, 이로부터 대부분의 bit (rate)가 인지하기 힘든 distortion을 수정하는데 할당된다는 것을 알 수 있다.
사실 이 관찰로부터 현재 SOTA architecture인 LDM이 시작된다. Diffusion model을 latent space에서 모델링함으로써, 인지하기 힘든 distortion에 diffusion step을 할당하는 것을 막고자 하는 것이다. 이는 후에 LDM을 다룰 때 다시 설명하겠다.
처음 생성 모델을 공부할 때, DDPM이 너무 어려워서 반년 가까이 시간을 투자했었다. 그래서 이번 포스팅을 굉장히 오랜 시간 작성하게 되었는데, 이후 논문들은 조금 간략하게 전달할 예정이다.
Leave a comment